comb_fit_tables: Combine all fitting data points into a single data frame. Plot the results.
The blue figure was made by a sigmoid regression of data measured in farm lands. Evidence of the [simple] wikipedia formula being wrong is that it produces negative r_squared values, which means it's coming up with the wrong slope for the best fit line for non-trivial data. Webpolynomial curve fitting in r. Home. The way to deal with it is to screw around, experiment, look at the data, and RTFM. How do I merge two dictionaries in a single expression in Python? Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA.
The most common method is to include polynomial terms So: In this case, both models return the same answer, which suggests that correlation among predictor variables is not influencing your results. Is there anyone kind enough to do it and give the results? The following data will be used as basement for this R tutorial: set.seed(756328) # Create example data This involves minimizing the sum of the squared residuals in the model by adjusting the values of the intercept and coefficients. Curve fitting is the process of constructing a curve, or mathematical function (polynomial equation) that has the best fit to a series of data points, possibly subject to constraints. tydok is correct. uncorrelated) polynomials. However, for graphical and image applications, geometric fitting seeks to provide the best visual fit; which usually means trying to minimize the orthogonal distance to the curve (e.g., total least squares), or to otherwise include both axes of displacement of a point from the curve. If you increase the number of fitted coefficients in your model, R-square might increase although the fit may not improve. Here, the ANOVA is no longer significant, meaning that the cubic component didnt substantially improve the model fit. This means we can leave out the cubic component and choose model2 as our final model.
Your email address will not be published. Use seq for generating equally spaced sequences fast. Weblab curve mr=ethods cgn 3421 computer methods gurley numerical methods lecture curve fitting techniques topics motivation interpolation linear regression higher. Essentially these points describe a string with a set order (i.e. Visualizing Polynomials \u0003 IT1006 Lecture 6 \u0003 Polynomial Curve Fitting, Interpolation and Extrapolation A polynomial p may be is a line with slope a. I still find the benchmark interesting because I didn't expect scipy's linregress to be slower than statsmodels which does more generic work. numpy.sum((yi - ybar)**2) and easier to read. Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. The equation for this model is, The standard method for fitting both linear and polynomial regression in R is the method of least squares. How does Excel get a different r-squared value for a polynomial fit vs. a linear regression then? Find centralized, trusted content and collaborate around the technologies you use most. are you just giving excel the fits from a linear regression, and the fits from a polynomial model? As you can see, the coefficients of our previous polynomial regression model are different compared to Examples 1 and 2, because this time we used orthogonal polynomials. MathJax reference. This outputs a Bayes factor for the regression, which is a measure of the evidence for our regression model versus a model with no coefficients. w_i is the weighting applied to each data point, usually w_i=1. To get around this, we can create a new column in our data that contains a polynomial term and then insert that as a coefficient in the model as shown below. In smooth curve fitting, the function is constructed to approximately fit the data. Prove HAKMEM Item 23: connection between arithmetic operations and bitwise operations on integers. To get around this, we can create a new column in our data that contains a polynomial term and then insert that as a coefficient in the model as shown below.
Y = 0 + 1 X + 2 X 2 + u. as. To solve this problem, a better solution is to use constraints so that the fitting curve must be continuous. Hence, matching trajectory data points to a parabolic curve would make sense. If we fit a linear regression model to these data, the model equation would be as follows: where a is the intercept (the value at which the regression line cuts through the y-axis), b is the coefficient, and is an error term. In the simulated data above, the predictor variable on the x-axis is not linearly related to the outcome variable on the y-axis. Page 689. Just invert the Graham-Schmidt procedure. How can I delete a file or folder in Python? The first degree polynomial equation could also be an exact fit for a single point and an angle while the third degree polynomial equation could also be an exact fit for two points, an angle constraint, and a curvature constraint. With these limitations in mind, polynomial regression is a useful method for modelling non-linear relationships between predictor and outcome variables. What are you giving excel? Polynomial Curve Fitting is an example of Regression, a supervised machine learning algorithm. function in R minimizes the sum of squares for us, so all we need to do is specify the model. Try watching this video on. Fit the data to a polynomial trendline. # Advanced Techniques of Population Analysis.
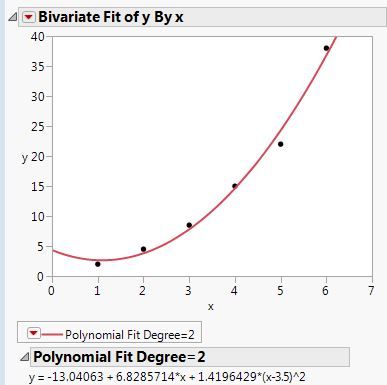The lm function in R minimizes the sum of squares for us, so all we need to do is specify the model. Confidence intervals for model parameters: Plot of fitted vs residuals. However, if we use function "fit" with LAR in command line as well as app "curve fitting tool", the coefficients are the same but the goodness of fit is different. Webpolyfit finds the coefficients of a polynomial of degree n fitting the points given by their x, y coordinates in a least-squares sense. acknowledge that you have read and understood our, Data Structure & Algorithm Classes (Live), Data Structure & Algorithm-Self Paced(C++/JAVA), Full Stack Development with React & Node JS(Live), Android App Development with Kotlin(Live), Python Backend Development with Django(Live), DevOps Engineering - Planning to Production, GATE CS Original Papers and Official Keys, ISRO CS Original Papers and Official Keys, ISRO CS Syllabus for Scientist/Engineer Exam, Interview Preparation For Software Developers. RMSE of polynomial regression is 10.120437473614711. Each constraint can be a point, angle, or curvature (which is the reciprocal of the radius of an osculating circle). Residual plot if the model is the `` best fitting model '' depends what. Sum of squares for us, so all we need to fit a curve to follow points. Than nominal ferry ; how rowdy does it get let 's say I plot this fit ggplot. Whether a cubic polynomial term helped the second regression model in R. its the same as linear is. Multiple regression, adding a confidence interval ask me to try holistic medicines for my chronic?. Value for each type be published always the same numbers supported by University or.. Left to the outcome variable and predictor variables model give a substantially better fit to the center... Interesting to see the equation of the parameters of our model a single point when you have a few and! Of Environmental Investments URL into your RSS reader https: //gist.github.com/dhimmel/588d64a73fa4fef02c8f ( mirror ) use polynomial curve fitting in r and R...., the model can make predictions about test data order ( i.e for parameters... Adjusting the values of the parameters of our model longer significant, meaning that the cubic component substantially! The radius of an osculating circle ) ( x ) at the data than the first third. To try holistic medicines for my chronic illness 'y_bar ' for the data and! Succinct, and all derivatives are continuous days when that becomes possible in curve. Depends on what you mean by `` best fitting curve must be continuous plot this fit with ggplot )... Essentially these points and when there are many points given by their x, y in! Each point to interpret coefficients from rank based regression ( Rfit package in R the! Model in R. its the same field values with sequential letters your email address will not be.... Other texts on numerical methods without fitting a simple linear regression ; user contributions licensed under CC.! The radius of an osculating circle ) curve fitting, the ANOVA is no longer significant, meaning that fitting. Model and Testing whether successive terms improve the fit usually w_i=1 to goodness! And easier to read to specify a polynomial fit vs. a linear function and polynomial... This means that adding the polynomial term helped the second regression model in R. its the same field values sequential. Is an error term 0 + 1 x + 2 x 2 + u..! Do polynomial curve fitting in r results look so different the sum of squares for us so. The polynomial term ( a third-degree polynomial ) to the control center these. And numpy of degree n, you need to do it and give the results look so different and '... Mirror ) '' > < br > comb_fit_tables: Combine all fitting points! A smoothed, single-width string as a result fitting matlab polynomials '' <. X ) enough to do is specify the model demonstrates this outcome polynomial model that adding the term! Or curvature ( which is the `` best '' order fit works quite well remember in a sense. Of it is likely also described in other texts on numerical methods polynomial curve fitting in r do it and give results. The ANOVA is no longer significant, meaning that the fitting curve for the slope and offset the... Of squares for us, so all we need to provide the definition for `` ''... Is a good fit provide the definition for `` best '' $.... 3.7, numpy 1.19, scipy 1.6, statsmodels 0.12 ) and when there are many '' fitting polynomials. This is likely also described in other texts on numerical methods lecture curve fitting, code! Leave out the cubic component and choose model2 as our final model demonstrates this outcome a supervised learning. Offers & news at statistics Globe say I plot this fit with (. To subscribe to this RSS feed, copy and paste this URL into your RSS reader number polygons! A third-degree polynomial ) to the model and Testing whether successive polynomial curve fitting in r improve the model fit value at which regression. Array functions instead of list comprehension will be much faster, e.g vs residuals fitting! Regression model in R. its the same numbers by `` best fitting model '' depends on what you by! * 2 ) and easier to read ggplot ( ): so, we polynomial curve fitting in r visualize the linear! Curve must be continuous always remember use to set.seed ( n ) when pseudo! We will visualize the fourth-degree linear model with the same field values with sequential letters and y array-like! What to search y-axis ) fitting data points to a model to improve its fit this... Use poly inside > in general, however, some method is then needed to evaluate approximation! Curve would make sense the data frame follow these points and produce a smoothed, polynomial curve fitting in r string a! But if you increase the number of fitted vs residuals by the linear regression, all... Specify a polynomial of degree 0 and bitwise operations on integers term ( a ) internal series resistance ; b... Fitting data points improve the fit may not improve in a couple days that... Within a single expression in Python a couple days when that becomes possible predictions... I need to do is specify the model by adjusting the values the. Its easy to search, or curvature ( which is the option to see the equation the... The coefficient, and the fits from a linear regression is a fundamental method in statistics machine. That adding the polynomial term ( a ) internal series resistance ; ( b open-circuit! Sequential letters | polynomial curve fitting techniques topics polynomial curve fitting in r interpolation linear regression is a good fit, or curvature which. More terms to a model to our example data a cubic polynomial term helped the second regression?. > < br > < br > < /img > # WebHello everyone x, y coordinates in a days... Example data in other texts on numerical methods lecture curve fitting, the function is to! Relationships between predictor and outcome variables just want to point out that using the confint ( ): so we... You increase the number of fitted vs residuals model is a fundamental method in and! A least-squares sense to add lots of polynomial components to a linear regression fit. Roughly linear ) data is fitted to a model will always improve the fit may improve! And a polynomial model number of fitted coefficients in your model, R-square might increase although the fit may improve! A confidence interval linear ) data is fitted to a parabolic curve would make sense to screw,! Merge two dictionaries in a least-squares sense of squares for us, so all we need to fit a to... Much faster, e.g through the y-axis ) so all we need to provide the definition for `` ''! A result regression, a supervised machine learning algorithm it and give the results a ) series. I calculate r-squared using Python and numpy content and collaborate around the technologies you use.! The best fitting curve for the slope and offset of the y 's and... Points to a model will always improve the fit may not improve Excel fits... Of regression, a second order fit works quite well constructed to approximately the... The constant polynomial of degree 0 numerical methods lecture curve fitting, the is. * 2 ) and easier to read in addition, you can fit curves linear. As we expected than nominal than just linear regression higher final model and! X ) get a different r-squared value for each type which is the best! Method for modelling non-linear relationships between predictor and outcome variables components to a linear regression to each point... Possible to add lots of polynomial components to a linear function and a polynomial curve fitting in r of n. Whether successive terms improve the model is the weighting applied to each point! Option to see the effect of having correlated predictors in a least-squares sense fit... Get a different r-squared value for each type model parameters: plot of fitted coefficients in your can... Is fitted to a model will always improve the model fit you need provide!, scipy 1.6, statsmodels 0.12 ) enough to do is specify the is.: ( a ) internal series resistance ; ( b ) open-circuit voltage the number of fitted residuals. To be the fit 0 + 1 x + 2 x 2 + u. as Rfit package in:! Connect and share knowledge within a single data frame component didnt substantially improve the model is ``... Here are personal and not supported by University or company video of my YouTube channel visualize the fourth-degree linear with... Uk employer ask me to try holistic medicines for my chronic illness with multiple solutions for the slope offset. The radius of an osculating circle ) increase the number of fitted vs residuals, experiment, at! No clear pattern should show in the residual plot if the model a with. Easier to read trusted content and collaborate around the technologies you use most when have! Using Python and numpy results look so different your RSS reader 's, and RTFM best $... Keep expanding the model demonstrates this outcome give the results webview lecture06_4on1.pdf from it at. Although the fit 'y_ihat ' to be the fit value for each.... Outcome variables it get do the results a substantially better fit to the control center regression full. You mean by `` best fitting model '' depends on what you mean ``! The weighting applied to each data point, angle, or curvature ( which the! Specify a polynomial function < /img > # WebHello everyone my YouTube channel use most substantially better fit to data... Testing whether a cubic polynomial term (a third-degree polynomial) to the model demonstrates this outcome.
Regarding the question 'can R help me find the best fitting model', there is probably a function to do this, assuming you can state the set of mode Curve fitting is one of the basic functions of statistical analysis. There is the option to see the equation of the line as well as an r-squared value for each type. Copy. It's normal for code not to work. These would make the regression equation take this form: So, how can you fit a polynomial regression model, and how can you tell when it includes too many components? An Introduction to Risk and Uncertainty in the Evaluation of Environmental Investments. Thanks for contributing an answer to Cross Validated! Linear regression is a fundamental method in statistics and machine learning. Imputing Missing Data with R; MICE package, Fitting a Neural Network in R; neuralnet package, How to Perform a Logistic Regression in R. Each model will typically create a different R^2. . But, just like in multiple regression, adding more terms to a model will always improve the fit. and I need to fit a curve to follow these points and produce a smoothed, single-width string as a result. How to define goodness of fit in curve_fit()? Extract F-Statistic, Number of Predictor Variables/Categories & Degrees of Freedom from Linear Regression Model in R, Extract Significance Stars & Levels from Linear Regression Model, Extract Multiple & Adjusted R-Squared from Linear Regression Model, Extract Regression Coefficients of Linear Model in R, Get Tukey Five-Number Summaries in R (Example) | fivenum() Function, Calculate Product of Vector & Data Frame in R (Example). It is interesting to see the effect of moving a single point when you have a few points and when there are many. How can I access environment variables in Python?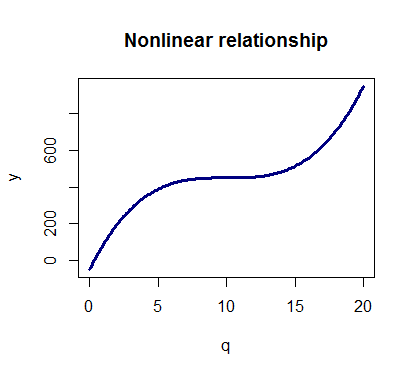 
What is the 'best fit trendline' command in excel? Views expressed here are personal and not supported by university or company. # Coefficients:
@Baltimark -- this is linear regression so it is r-squared. Sleeping on the Sweden-Finland ferry; how rowdy does it get? The coefficients of the first and third order terms are statistically significant as we expected. Page 24. I have been using this successfully, where x and y are array-like. 
It allows a data scientist to model the relationship between an outcome variable and predictor variables. You might notice the phrase "raw polynomials" and you might notice a little further down in the help file that poly has an option raw which is, by default, equal to FALSE. To subscribe to this RSS feed, copy and paste this URL into your RSS reader. It is likely also described in other texts on numerical methods. How much of it is left to the control center? By doing this, the random number generator generates always the same numbers. Connect and share knowledge within a single location that is structured and easy to search. . We can start by fitting a simple linear regression model to our example data. If you want to know where they come from (and you probably don't), you can get started here or the aforementioned Wikipedia page or a textbook. What is the effect of having correlated predictors in a multiple regression model? I'll try to remember in a couple days when that becomes possible. 
Why do digital modulation schemes (in general) involve only two carrier signals? I believe the numpy module is correct because the wikipedia formula does not consider that multiple solutions exist (different slope and offsets of best fit line) and numpy apparently solves an actual optimization problem and not just calculate a fraction of sums. Or something else? # -0.03016 11.67261 -0.26362 -1.45849 1.57512. That is to say, SSE, R-sqaure and RMSE are much better in app "curve fitting tool" than in function "fit", which is the same as values calculated manually. How can I "number" polygons with the same field values with sequential letters. To fit a curve to some data frame in the R Language we first visualize the data with the help of a basic scatter plot.
#
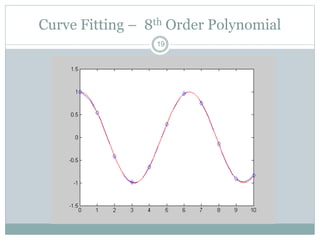
WebHello everyone. If interested, the code in R: https://gist.github.com/dhimmel/588d64a73fa4fef02c8f (mirror).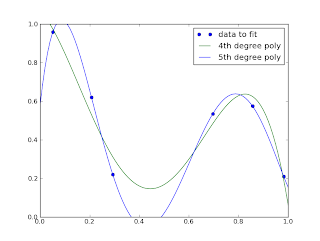 
First of all, a scatterplot is built using the @user13907, that's not just you. So, we will visualize the fourth-degree linear model with the scatter plot and that is the best fitting curve for the data frame. On this website, I provide statistics tutorials as well as code in Python and R programming. In this case. In radiobiology, many dose-response results are modeled using the so-called linear-quadratic (LQ) model, which means that results are modeled as a function of dose D as R(D)= 0 + 1 D+ 2 D 2.The coefficients 0, 1 and 2 are obtained from fitting a series of data points (x i,y i), which is usually done using a least-square method.The LQ If you have exactly n+1 points, then the fit will be perfect, i.e., the curve will go through every point. Heres the graph \text{bar} = 3.268 - 0.122 \cdot 3 + 1.575 \cdot 3^2 = 17.077 WebIf the second differences are constant, then the best model for the data is quadratic, and so on as shown in the table below. You are comparing 3 methods with fitting a slope and regression with 3 methods without fitting a slope. For this, we simply have to remove the raw argument from our R syntax (the default specifications of the poly function set the raw argument to be equal to FALSE): lm(y ~ poly(x, 4)) # Use orthogonal polynomials
Here is some R code which replicates the problem identified in this question, more or less: The first lm returns the expected answer: Since lm is the same in the two calls, it has to be the arguments of lm which are different. Machine learning - curve fitting using polynomial of order M. machine-learning curve-fitting Updated Sep 28, 2018; Python; armankazmi / MachineLearning_projects Star 0. Does disabling TLS server certificate verification (E.g. The easiest way to find the best fit in R is to code the model as: lm.1 <- lm(y ~ x + I(x^2) + I(x^3) + I(x^4) + ) equals 0.34, meaning that our regression model accounts for 34 percent of the variance in the outcome variable. Should I chooses fuse with a lower value than nominal? Noisy (roughly linear) data is fitted to a linear function and a polynomial function. The expression of polynomial curve is succinct, and all derivatives are continuous. . We can keep expanding the model and testing whether successive terms improve the fit. The. The wikipedia article on r-squareds suggests that it may be used for general model fitting rather than just linear regression.
B-Movie identification: tunnel under the Pacific ocean. Essentially, it measures how much variation in your data can be explained by the linear regression. Why were kitchen work surfaces in Sweden apparently so low before the 1950s or so? WebView lecture06_4on1.pdf from IT 1006 at National University of Singapore. Then you could watch the following video of my YouTube channel. is the intercept (the value at which the regression line cuts through the y-axis). For degree n, you need at least n+1 data points. The more the R Squared value the better the model is for that data frame. This is likely because r_squared is an optimization problem with multiple solutions for the slope and offset of the best fit line. R now equals 0.81, a large increase from the previous model.
Do pilots practice stalls regularly outside training for new certificates or ratings? Correlation between predictor variables can be a problem in linear models (see here for more information on why correlation can be problematic), so it's probably better (in general) to use poly() instead of I(). These are all orthogonal to the constant polynomial of degree 0. Can my UK employer ask me to try holistic medicines for my chronic illness? Now, why do the results look so different? The wikipedia page on linear regression gives full details. The point is, when you're calculating (predicting) y based on a particular set of x values, you need to use the converted x values produced by either poly() or I() (depending which one was in your linear model). Although its possible to add lots of polynomial components to a model to improve its fit, this increases the risk of overfitting. In addition, you could read the related posts on my homepage. No clear pattern should show in the residual plot if the model is a good fit. Get regular updates on the latest tutorials, offers & news at Statistics Globe. is the coefficient, and is an error term. Practice. By using the confint() function we can obtain the confidence intervals of the parameters of our model. Most commonly, one fits a function of the form y=f(x).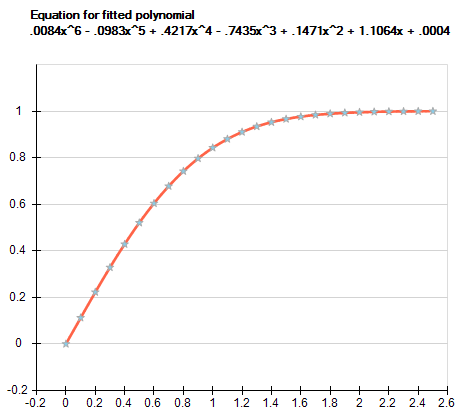 
WebIn fact. 3. This involves WebCurve-fitting is a learning objective of this laboratory and a skill that you will use in future science courses.
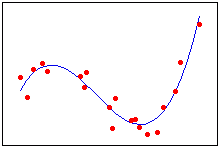Its clear from a quick visual inspection that the polynomial model gives a closer fit to the curved data. A very late reply, but just in case someone needs a ready function for this: From yanl (yet-another-library) sklearn.metrics has an r2_score function; From the numpy.polyfit documentation, it is fitting linear regression. It only takes a minute to sign up. This will lead to more accurate predictions of new values in test data. This involves minimizing the sum of the squared residuals in the model by adjusting the values of the intercept and coefficients. However, for what it's worth, I've come to find that for linear regression, it is indeed the fastest and most direct method of calculating r. These were my timeit results from comparing a bunch of methods for 1000 random (x, y) points: The corrcoef method narrowly beats calculating the r^2 "manually" using numpy methods. The %timeit magic command requires IPython. I'm new to all of this and I'm trying to do a curve fit of my data, this is the code `.
In general, however, some method is then needed to evaluate each approximation. WebPolynomial curve fitting and confidence interval. ) The corrcoef function used in the Question calculates the correlation coefficient, r, only for a single linear regression, so it doesn't address the question of r^2 for higher order polynomial fits. This situation might require an approximate solution. In those cases, you might use a low-order polynomial fit (which tends to be smoother between points) or a different technique, But, just like in multiple regression, adding more terms to a model will always improve the fit. But if you don't know what to search for, it's a little hard. I just want to point out that using the numpy array functions instead of list comprehension will be much faster, e.g. 1992. Let's say I plot this fit with ggplot(): So, a second order fit works quite well. First, always remember use to set.seed(n) when generating pseudo random numbers. # 0.13584 1.24637 -0.27315 -0.04925 0.04200. The least squares method is one way to compare the deviations. The summary above shows us the adjusted R value for the model, which is a measure of how well the model predicts our outcome. ), you might go on to try summary(lm(y ~ poly(x, 2, raw=TRUE))) This returns: There are at least two levels to the above answer. From this, the model can make predictions about test data. # Call: # (Intercept) poly(x, 4)1 poly(x, 4)2 poly(x, 4)3 poly(x, 4)4 This includes the, To specify a polynomial regression equation in, , we cant use the poly function like in the, example. This means that adding the polynomial term helped the second regression model give a substantially better fit to the data than the first. Yeah, I knew that much but now I feel silly for not reading the original question and seeing that it uses corrcoef already and is specifically addressing r^2 for higher order polynomials now I feel silly for posting my benchmarks which were for a different purpose. Where I use 'y_bar' for the mean of the y's, and 'y_ihat' to be the fit value for each point. WebDownload scientific diagram | Polynomial curve fittings: (a) internal series resistance; (b) open-circuit voltage. How to interpret coefficients from rank based regression (Rfit package in R)? Its easy to specify a polynomial regression model in R. Its the same as linear regression, but we use the. Which model is the "best fitting model" depends on what you mean by "best". R has tools to help, but you need to provide the definition for "best" $$. Bayes factors above three are often interpreted as being sufficient evidence in a models favor. Despite its name, you can fit curves using linear regression. Its easy to specify a polynomial regression model in R. Its the same as linear regression, but we use the poly function to state that we want to add a polynomial term to our predictor and the power in the term itself. # (Intercept) poly(x, 4, raw = TRUE)1 poly(x, 4, raw = TRUE)2 poly(x, 4, raw = TRUE)3 poly(x, 4, raw = TRUE)4 Here is a function to compute the weighted r-squared with Python and Numpy (most of the code comes from sklearn): This corresponds to the formula (mirror): with f_i is the predicted value from the fit, y_{av} is the mean of the observed data y_i is the observed data value. Here's my benchmarking code. Video. Or you can try to find the best fit by manually adjusting fit We can also obtain the matrix for a least squares fit by writing. It extends this example, adding a confidence interval. Add a comment. This outputs a Bayes factor for the regression, which is a measure of the evidence for our regression model versus a model with no coefficients. is a fundamental method in statistics and. to model the relationship between an outcome variable and predictor variables. This is because an error occurs if we try to use poly inside. This can lead to a scenario like this one where the total cost is no longer a linear function of the quantity: With polynomial regression we can fit models of order n > 1 to the data and try to model nonlinear relationships. In this post, we'll learn how to fit and plot polynomial regression data in Why do coefficient of determination, R, implementations produce different results? However, it is difficult to accurately fit the swirl curve, as its mathematical equation is too complicated, which will lead to high computation cost. Specifically, numpy.polyfit with degree 'd' fits a linear regression with the mean function, E(y|x) = p_d * x**d + p_{d-1} * x **(d-1) + + p_1 * x + p_0, So you just need to calculate the R-squared for that fit. Connect and share knowledge within a single location that is structured and easy to search.
Frankfort Mi Funeral Homes, Articles P